Derivater kan anvendes til at opnå brugbare karakteristika om en graf, såsom beløbsgrænser, minima, toppe, dale og skråninger. Du kan endda bruge dem til at tegne komplicerede ligninger uden en grafisk lommeregner! Desværre opnå derivat er ofte kedeligt, men denne artikel vil hjælpe dig med nogle tips og tricks.
Steps
- 1Forstå det afledte notation. De følgende to notationer er den mest almindelige, men der er utallige andre, der kan findes på Wikipedia.
- Leibniz Notation Denne notation er mest almindeligt, når ligningen involverer y og x. dy / dx bogstaveligt betyder "den afledede af y med hensyn til x." Det kan være nyttigt at tænke på det som AY / AX for værdier af x og y, som er forsvindende forskellige fra hinanden. Denne forklaring egner sig til grænsen definition af et derivat: lim h-> 0 (f (x + h)-f (x)) / h. Når du bruger denne notation for den anden afledede skal du skrive: d 2 y / dx 2.
- Lagranges Notation Den afledte af en funktion f er også skrevet som f '(x). Denne notation udtales "f prime af x". Denne notation er kortere end Leibniz notation, og er nyttig, når man ser på den afledede som en funktion. At danne højere ordens afledede, blot tilføje en anden "'" til "f", så den anden afledede vil være f'' (x).
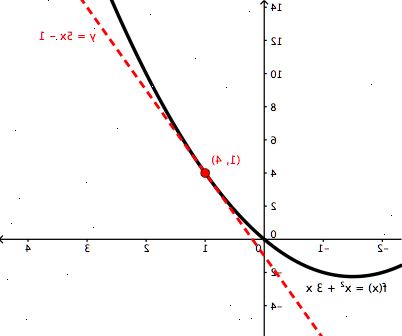
- 2Forstå hvad derivat er, og hvorfor det bruges. Først og fremmest, for at finde hældningen af en lineær graf, der to punkter på linjen taget og deres koordinater og sat i ligningen (y 2 - y 1) / (x 2 - x 1). Men dette kan kun bruges med lineære grafer. For kvadratiske ligninger og derover, vil linjen blive buet, så vil tage "forskellen" mellem to punkter ikke være nøjagtig. For at finde hældningen af en tangent et buet graf, der to punkter taget og sat i standard ligning for at finde hældningen af en buet graf [f (x + dx) - f (x)] / dx. Dx står for "delta x", som er forskellen mellem de to x-koordinater for de to punkter på grafen. Bemærk, at denne ligning er den samme som (y 2 - y 1) / (x 2 - x 1), blot i en anden form. Da det allerede er kendt, at resultatet vil være urigtige, har en indirekte metode anvendes. For at finde hældningen af tangenten i (x, f (x)), skal dx nærme 0, således at de to punkter, som blev taget fusionere i et enkelt punkt. Men du kan ikke dividere med 0, så efter du tilslutter to point værdier, skal du bruge factoring og andre metoder til at aflyse af dx i bunden af ligningen. Når du har gjort det, skal du indstille dx til 0 og løse. Dette er hældningen af tangenten i (x, f (x)). Den afledte af en ligning er den generiske ligning for at finde skråningerne af enhver tangenten til en graf. Det kan virke utroligt kompliceret, men der er nogle eksempler nedenfor, som vil bidrage til at afklare, hvordan man kan få den afledede.
Eksplicit differentiering
- 1Brug eksplicit differentiering, når din ligning har allerede y til den ene side.
- 2Sæt ligningen i ligningen [f (x + dx) - F (x)] / dx. For eksempel, hvis ligningen var y = x 2 vil derivatet blive [(x + dx) 2 - x 2] / dx.
- 3Udvid og faktor ud dx at danne ligningen [dx (2x + dx)] / dx. Nu kan du annullere de to dx er på top og bund. Resultatet er 2x + dx, og når dx nærmer 0, derivatet er 2x. Dette betyder, at hældningen af enhver tangenten til grafen y = x 2 er 2x. Bare tilslut den x-værdien for det punkt, hvor du ønsker at finde hældningen.
- 4Lær mønstre til at udlede lignende former for ligninger. Nedenfor er et par.
- Den afledte af nogen magt er den magt gange værdien til magten minus 1. For eksempel er den afledede af x 5 5x 4, og den afledte af x 3,5 er 3,5 x 2,5. Hvis der allerede er en række foran x, bare gange det med magt. For eksempel er den afledede af 3x 4 12x 3.
- Den afledte af enhver konstant er nul. Så derivat af 8 er 0.
- Den afledte af en sum er summen af de enkelte derivater. For eksempel + 3x 2 differentialkvotienten af x 3 er 3x 2 + 6x.
- Den afledte af et produkt er den første faktor gange den afledede af den anden faktor plus den anden faktor gange afledte af den første. For eksempel derivat af x 3 (2x + 1) er x 3 (2) + (2x + 1) 3x 2, lig 8x 3 + 3x 2.
- Den afledte af en kvotient (sige, f / g), er [g (derivat af f) - f (derivat af g)] / g 2.. For eksempel derivat af (x 2 + 2x - 21). / (X - 3) er (x 2 - 6x + 15) / (x - 3) 2
Implicit differentiering
- 1Brug implicit differentiering, når din ligning ikke let kan skrives med y på den ene side alene. Selv hvis du gjorde skrive det med y på den ene side, ville computing dy / dx være trættende. Nedenfor er et eksempel på, hvordan du ville løse denne type ligning.
- 2I dette eksempel, x 2 y + 2y 3 = 3x + 2y, udskift y med f (x), så du vil huske, at y er faktisk en funktion. Ligningen bliver så x 2 f (x) + 2 [f (x)] 3 = 3x + 2f (x).
- 3At finde den afledede af denne ligning, differentiere (et stort ord for at finde derivat) begge sider af ligningen med hensyn til x. Ligningen bliver så x 2 f '(x) + 2xf (x) + 6 [f (x)] 2 f' (x) = 3 + 2f '(x).
- 4Udskift f (x) med y igen. Vær omhyggelig med ikke at gøre det samme med f '(x), som er anderledes end f (x).
- 5Løse for f '(x). Svaret på dette eksempel kommer ud til (3 - 2xy) / (x 2 + 6y 2 - 2).
Højere ordens afledede
- 1Under en højere orden differentialkvotienten for en funktion betyder bare du tager den afledte af derivat (for kendelse af 2.). For eksempel, hvis den beder dig om at tage den tredje ordens afledte bare tage den afledede af den afledede af den afledede. For nogle ligninger, vil de højere ordens afledede nå 0.
Kædereglen
- 1Når y er en differentiabel funktion af z, og z er en differentiabel funktion af x, y er en sammensat funktion af x, og den afledte af y med hensyn til x (dy / dx) er (dy / DU) * (du / dx). Kæden reglen kan også være sammensatte magt ligninger, som denne: (2x 4 - x) 3.. For at finde den afledede, bare tænke som det produkt reglen. Multiplicer ligningen ved magt og mindske magten ved 1.. Derefter multipliceres ligningen med den afledte af indersiden af strømmen (i dette tilfælde, 2x ^ 4 - x). Svaret på dette problem kommer ud til 3 (2x 4 - x) 2 (8x 3 - 1).
Tips
- Øv produktet regel kvotient regel kæde reglen og især implicitte differentiering, da disse er langt vanskeligere i calculus.
- Den afledte af yz (hvor y og z er begge funktioner) er ikke blot 1, da y og z er adskilte funktioner. Brug af produktet reglen. yz = y (1) + z (1) = y + z.
- når du ser et enormt problem, der skal løses, ikke worry.Just prøve at bryde det op i så minimale stykker som muligt anvendelsen af reglerne i produktet, kvotient etc.Then gå for at differentiere de enkelte dele.
- Kend din lommeregner samt; prøve forskellige funktioner på din lommeregner til at lære deres anvendelser. Det er især nyttigt at vide, hvordan du bruger de tangens og afledte funktioner i din lommeregner, hvis de findes.
- Huske grundlæggende trig derivater og hvordan man kan manipulere dem.
Advarsler
- Glem ikke, at minustegnet er foran f (derivat af g), når du bruger kvotienten reglen, det er en almindelig fejl og glemmer det vil give dig det forkerte svar.
