Dette vil lære dig at tegne punkter på et koordinatsystem plan (x, y-format), samt hvordan man kan læse formler og ændre din graf til at passe.
Steps
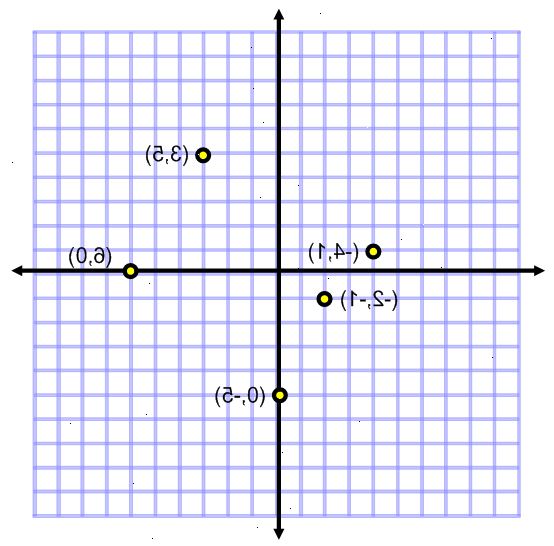
For enlige point
- 1Find den første koordinat i et ordnet par er på x-aksen.
- X-aksen går til venstre og højre, den anden koordinat er på Y-aksen.
- Y-aksen går op og ned.
- Positive tal gå op eller til højre (afhængigt aksen). Negative tal gå til venstre eller ned.
- 2Bestem kvadrant punktet er i.
- Husk, at en graf har fire kvadranter (typisk mærket med romertal). Kvadrant I får (+, +), kvadrant I er over og til venstre for Y-aksen. Kvadrant IV får (+, -), kvadrant IV ligger under x-aksen og til højre for Y-aksen. (5,4) er i kvadrant I. (-5,4) er i kvadrant II. (-5, -4) Er i kvadrant III. (5, -4) er i kvadrant IV.
- 3Markér punktet.
For grafer af linier, cirkler, parabler osv.
- 1Bestemme, hvilken form din grafen vil tage. Vil det være en linje, parabel, cirkel, etc.
- Dette afsnit vil ikke lære dig at tegne en linje, parabel, osv. Du skal lære, at i klassen. Dette vil hjælpe dig til at ændre din grafen for at det passer til situationen. Hvis du laver disse grafer for første gang, grafen dem ved hjælp af en række punkter.
- Din lærer vil ikke være interesseret i dig plotte præcise punkter i den slags grafer. Du lærer vil være interesseret i, om du ved, hvordan man finde (og identificere) disse punkter. Din lærer vil være på udkig efter en graf for den korrekte form, kvadrant (r), orientering, hældning, og at de vigtige punkter er noteret.
- 2Bestem, hvilke punkter, du vil medtage på grafen. Komplekse grafer kræver flere point.
- Medmindre du kun graftegning et punkt, vil du bruge mindst to punkter. En linje kræver to punkter. En cirkel kræver to point, hvis man er centrum, tre, hvis centret ikke er inkluderet (Medmindre din instruktør har medtaget i midten af cirklen i problemet ved at bruge tre). En parabel kræver tre point, det ene er et absolut minimum eller maksimum, de to andre punkter bør være modsætninger. En hyperbel kræver seks point, tre på hver akse.
- 3Forstå hvordan ændrer ligningen ændrer grafen.
- Ændring af variablen X bevæger ligningen til venstre eller højre.
Dreje det Negative (multiplikation med -1) vender det over, hvis det er en linje, vil det ændre den fra at gå op til ned eller gå ned til op. - Betragt ligningen y = x ^ 2, en parabel med sin base på (0,0).
y = (x-2) ^ 2 er den samme parabel, medmindre det er tegnet to rum til højre for oprindelse sin base er nu på (2,0).
y =-x ^ 2 (den negative påføres efter eksponenten ^ 2) er en upside down y = x ^ 2, sin base er (0,0).
y = 5x ^ 2 er stadig en parabel, men det bliver større endnu hurtigere, giver det en tyndere look.
- Ændring af variablen X bevæger ligningen til venstre eller højre.
Tips
- Hvis du vil lave disse, vil du højst sandsynligt nødt til at læse dem også. En god måde at huske at gå langs x-aksen først og y det andet, er at foregive, at du er ved at opbygge et hus, og du er nødt til at bygge fundamentet (langs x-aksen) knytnæve, før du kan bygge op. Det er den samme den anden vej, hvis du gå ned, foregive du gør kælderen. Du har stadig brug for en fond, og til at starte på toppen.
- En god måde at huske hvilken akse er der er at forestille sig den lodrette akse, der har en lille skrå linje på det, gør det til at ligne et "y".
- Akser er dybest set vandrette og negative tal linjer med både krydsende på oprindelsen (oprindelsen på et koordinatsystem fly er nul, eller hvor begge akser skærer hinanden). Everything "stammer" fra oprindelsen.
