Sådan bruger Pythagoras 'sætning

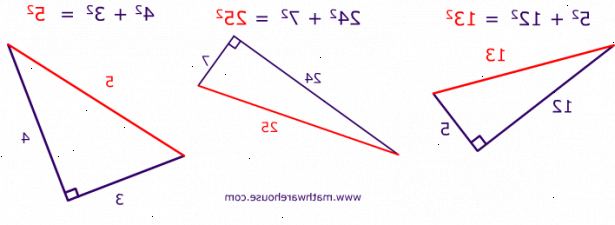
På retvinklede trekanter

1. 1
   Skriv ud pythagoræiske læresætning: a ² + b ² = c ², og tegne et billede af trekanten, du løser.
2. 2
   Mærk din tegning. Mærk kortere sider 'a' og 'b' (betyder ikke noget, hvilken side er a eller b), og mærke hypotenusen (den længste side, overfor den rette vinkel) »c '.
3. 3
   Afgøre, hvilken side af trekanten, du løser for: a, b, eller c.. Typisk vil du blive givet to af side længder og bruge formlen til at løse for den tredje.
4. 4
   Omskrive ligning med de kendte værdier.
   • Hvis du får de to side længder (siger 3 og 4), skriver:
     3 ² + 4 ² = c ²
   • Hvis du får den ene side og hypotenusen (3 & 5), skriver:
     3 ² + b ² = 5 ²
5. 5
   Beregn firkanter.
   • Det første eksempel ovenfor skal omskrives: 9 + 16 = c ².
   • Den anden: 9 + b ² = 25.
6. 6
   Kombiner lignende udtryk.
   • I dette tilfælde alle de vilkår på venstre side af ligningen er konstante, så vi kan tilføje dem til at få: 25 = c ².
   • I det andet eksempel, du bliver nødt til at trække 3 ² fra begge sider af ligningen at isolere variablen.
7. 7
   Tag kvadratroden.
   • Efter at tage kvadratroden af ​​begge sider af ligningen, er du tilbage med:
     c = 5.

Eksempel: Givet at hypotenusen er 10, og det ene ben er 8, finde længden af det andet ben.

a ² + b ² = c ²

(8) ² + b ² = (10) ²

64 + b ² = 100

b ² = 100-64

b ² = 36

b = kvadratroden af ​​36

b = 6

Eksempel: En stige læner sig op mod en bygning. Bunden af ​​stigen er 5 meter fra bunden af ​​væggen. Stigen når 20 meter op væg af bygningen. Hvor lang er stigen?

"5 meter fra bunden af ​​muren", en = 5
"Når 20 meter op ad væggen" forstås b = 20
stigen længde er hypotenusen, så c er ukendt

a ² + b ² = c ²

(5) ² + (20) ² = c ²

25 + 400 = c ²

425 = c ²

c = kvadratroden af ​​425

c = 20,6 (afrundet til nærmeste tiendedel)

Så den omtrentlige varighed af stigen er 20,6 meter.

Som en del af afstanden formel

Afstanden formel anvendes i geometri at finde den rette linje afstand mellem to punkter.

1. 1
   Beslut hvad peger bruge. Typisk punkter er givet som bestilte par.
2. 2
   Plotte punkter på en graf. (X, y), hvor x er den vandrette akse, og y er lodret.
3. 3
   Find længden af siderne af trekanten. Du kan gøre dette ved at tælle forskellen på grafen, eller ved at bruge (x ₁ - x ₂₎ for x og (y ₁ - y ₂₎ til y.
4. 4
   Brug det pythagoræiske læresætning. Afstanden mellem punkterne er hypotenusen af ​​trekanten.

Eksempel:
3. - 6. = -3 (x)
(-3) ² + (4) ² = c ²
c = sqrt (25)

På ikke-retvinklede trekanter ved hjælp af trigonometri

Dette afsnit bruger eksemplet med de to byer fra oven, i dette tilfælde er du nødt til at løse for afstanden fra City A til City C.
For dette eksempel antager sider 'a' og 'b' er kendte (se tegning nedenfor).

1. 1
   Tegn et billede af din trekant.
2. 2
   Tegn højden. En højde er en linje vinkelret på hypotenusen, der passerer gennem den modsatte toppunkt. I dette tilfælde højden er »c«.
3. 3
   Måle vinklen mellem linjen forbinder byen A til B og højden linje.
   
   • Typisk vinklen vil blive givet på denne form for problem. Hvis ikke, måle vinklen ved hjælp af en vinkelmåler.
4. 4
   Brug den trigonometriske funktion for at finde længden af højde:
   Hvis længden »a« er kendt, så: Cos (A) = c / a og c = ACOS (A)
5. 5
   Brug Pythagoras sætning til at finde længden af linjen fra byen A til højde:
   x1 = sqrt (a ² - c ²⁾
6. 6
   Brug Pythagoras sætning til at finde afstanden mellem højde linjen og by C: x2 = sqrt (b ² - c ²⁾
7. 7
   Tag summen af x1 og x2.
8. 8
   Eksempel: Du bor i byen A og har en ven der bor i byen C, og du ønsker at vide, hvor langt din ven bor fra dig. Du kender dens om en 50 mile drive til City B, yderligere 100 miles derfra til City C. derefter Hvor længe er en lige linje fra City A til City C? (Afrund alle beregninger til nærmeste tiendedel)
   
   • Tegn højden linje og måle vinklen.
     
   • Brug cosinusfunktionen at finde længden af ​​højden:
     længde = 50 x cos (30) = 50 x 0,866 hvilke runder til 43,3 miles
   • Brug Pythagoras 'læresætning til at finde længden af ​​x1:
     x1 = sqrt (50 ^{2-43,3 2)} = sqrt (625,11) = 25,0 miles
   • Brug Pythagoras 'læresætning til at finde længden af ​​afstanden x2:
     x2 = sqrt (100 ^{2-43,3 2)} = sqrt (8125,1) = 90,1 miles
   • Tilsæt de to distancer sammen for at finde den samlede distance:
     

I vektoraddition

Pythagoras 'læresætning anvendes ved løsning til nedfaldne vektorer. Dette gøres ved at bryde vektorerne i 'x' og 'y' komponenter (og »z 'i 3d), og tilføje lignende komponenter. De resulterende komponenter (siderne af retvinklet trekant) kan anvendes til at løse for den resulterende (hypotenusen).

1. 1
   Break dine vektorer i x-og y-komponenter. Vektorer har retning og omfang; retningen er vinklen skabt uret fra den positive x-aksen, og størrelsen er længden af ​​vektoren. For at bryde vektoren i komponenter, vil du bruge trigonometri. For eksempel kan en vektor med en størrelse 'M' og vinkel '30 ':
   • x = M * cos (30)
   • y = M * sin (30)
2. 2
   Tilføj ens komponenter. Nu hvor dine vektorer brudt ind x-og y-komponenter, tage summen af ​​x-komponenter og summen af ​​y-komponenter. Disse er de sider af trekanten.
3. 3
   Brug det pythagoræiske læresætning. I dette tilfælde (summen af ​​x) ² + (summen af ​​y) ² = c ², hvor 'c' er den resulterende størrelse.

Eksempel:
[10cos (30) + 15cos (45)] = 19.27 (afrundet til nærmeste hundrededel) (x)
(19.27) ² + (15.61) ² = c ²
c = sqrt (615,005)