Beregning af inverse en lineær funktion er let: bare gøre x emnet af ligningen, og erstatte y med x i den resulterende udtryk. Finde den inverse en kvadratisk funktion er betydeligt vanskeligere, ikke mindst fordi kvadratiske funktioner ikke, med mindre begrænset af en passende domæne, en-en-funktioner.
Steps
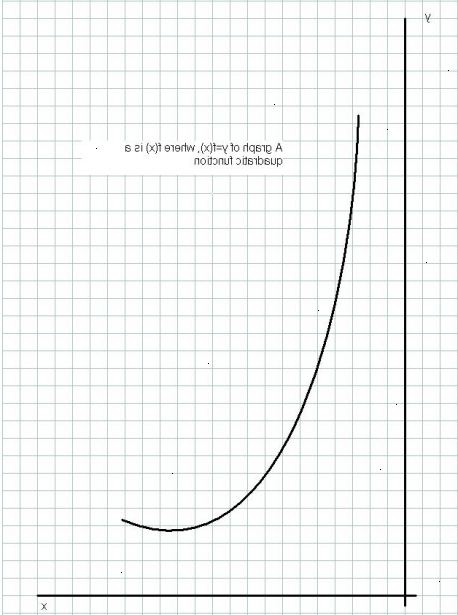
- 1Gør y eller f (x) er genstand for den formel, hvis det ikke allerede er. Under dit algebraisk manipulation, så sørg for at du ikke ændre funktionen på nogen måde og udføre de samme operationer på begge "sider" af ligningen.
- 2Omarrangere den funktion, således at det er på formen y = a (xh) 2 + k. Dette er ikke kun vigtigt for dig at finde den inverse funktion, men også for dig at afgøre, om den funktion har endda en invers. Du kan gøre dette ved to metoder:
- Ved at udfylde pladsen
- "Take fælles" fra hele ligningen værdien af en (koefficienten x 2). Gør dette ved at skrive værdien af en, der starter en konsol, og skrive det hele ligningen, og derefter dividere hver valgperiode med værdien af a, som vist i diagrammet til højre. Lad venstre side af ligningen uberørt, da der ikke har været nogen nettoændring i højre side.
- Udfyld pladsen. Koefficienten for x er (b / a). Halvere det, for at give (b/2a), og firkantet det, for at give (b/2a) 2. Tilføje og trække det fra ligningen. Dette vil ikke have nogen nettovirkning på ligningen. Hvis man ser nøje efter, vil du se, at de første tre betingelser inde i beslaget er i form en 2 +2 ab + b 2, hvor a er x, og b er (b/2a). Naturligvis disse to værdier vil være numerisk, i stedet algebraical for en reel ligning. Dette er en færdig firkant.
- Fordi de første tre begreber er nu en perfekt kvadrat, kan du skrive dem i form (ab) 2 eller (a + b) 2. Tegnet mellem de to begreber vil være den samme som fortegnet af koefficienten x i ligningen.
- Tag ordet som er uden den perfekte kvadrat ud af pladsen beslaget. Dette bringer ligning i formen y = a (xh) 2 + k y = a (xh) 2, som tilsigtet.
- Ved at sammenligne koefficienter
- Danne en identitet i x. Til venstre, satte den funktion, som det er udtrykt i x, og på højre sætte funktionen i den form, du ønsker det skal være, i dette tilfælde en (xh) 2 + k a (xh) 2.. Dette vil gøre det muligt for dig at finde ud af de værdier af a, h og k, der er sande for alle værdier af x.
- Åbn og udvide beslaget på højre side af identiteten. Vi skal ikke røre den venstre side af ligningen, og kan udelade det fra vores arbejde. Bemærk, at alle arbejder på højre side er algebraical som vist og ikke numerisk.
- Identificer koefficienterne for hver strøm af x. Så gruppere dem og placere dem i parentes, som vist til højre.
- Sammenlign koefficienterne for hver strøm af x. Den koefficient på x 2 på højre side skal svare at på den venstre side. Det giver værdien af en. Koefficienten x på højre side også skal svare, at der på venstre side. Dette fører til dannelsen af en ligning i et og h, som kan løses ved at erstatte værdien af en, der allerede er blevet fundet. Koefficienten x 0 eller 1, på den venstre side skal også lig at på den højre side. Sammenligne dem giver en ligning, der vil hjælpe os med at finde værdien af k.
- Ved anvendelse af værdierne a, fandt h og k ovenfor, kan vi skrive ligningen i den ønskede form.
- 3Sørg for, at værdien af h er enten på grænsen af domænet, eller udenfor. Værdien af h giver x-koordinat vendepunkt af ligningen. Et vendepunkt inden for domænet ville betyde, at funktionen ikke er en-en, og derfor ikke har en invers. Bemærk, at ligningen er en (x -H) 2 + k. Hvis der således er (x +3) inde i beslaget, værdien af h er negativ 3..
- 4Mærke (xh) 2. emnet for din formel. Gøre dette ved at trække værdien af k fra begge sider af ligningen, og derefter dividere begge sider af ligningen med en. Ved nu du vil have numeriske værdier for a, h og k, så brug dem, ikke symbolerne.
- 5Square-root begge sider af ligningen. Dette vil fjerne magt to fra (xh). Glem ikke at sætte "+ / -" skilt på den anden side af ligningen.
- 6Beslut mellem + og - Sign, som du ikke kan have både (med begge ville gøre det til en en til mange "funktion", hvilket ville gøre den ugyldig, da den samme). Til dette, se på domænet. Hvis domænet ligger til venstre for den stationære punkt dvs x <en vis værdi, skal du bruge tegnet -. Hvis domænet ligger til højre for den stationære punkt dvs x> en bestemt værdi, skal du bruge tegnet +. Så gør x genstand for formlen.
- 7Erstat y med x, og x med f -1 (x), og lykønske dig selv på at have held fundet den inverse en kvadratisk funktion.
- Ved at udfylde pladsen
Tips
- Hvis det ikke er for meget besvær kan du også tjekke den inverse ved at inspicere dens graf. Det skal se ud som den oprindelige funktion afspejles over linjen y = x.
- Tjek din inverse ved beregning af værdien af f (x) for en bestemt værdi af x, og derefter erstatte den pågældende værdi af f (x) i den inverse at se om det returnerer den oprindelige værdi af x. For eksempel, hvis funktionen af 3 [f (3)] er 4 bør derefter benyttede 4 i den inverse returnere 3..
