Dette er en artikel om, hvordan du faktorisere en 3 rd gradspolynomiet. Vi vil undersøge, hvordan man faktor bruge gruppering samt bruge de faktorer i det fri sigt.
Steps
Del 1: factoring ved at gruppere
- 1Gruppe polynomiet i to sektioner. Gruppering polynomiet i to sektioner vil lade os angribe hver sektion individuelt.
- Sige, at vi arbejder med polynomiet x 3 + 3x 2 - 6x - 18 = 0. Lad os gruppe det ind (x 3 + 3x 2) og (- 6x - 18)
- 2Find hvad der er almindeligt i hvert afsnit.
- Ser man på (x 3 + 3x 2), kan vi se, at x 2 er fælles.
- Ser man på (- 6x - 18), kan vi se, at -6 er fælles.
- 3Faktor fællestræk af de to begreber.
- Udskille x 2 fra den første sektion, vi får x 2 (x + 3).
- Factoring ud -6 fra den anden sektion, vi får -6 (x + 3).
- 4Hvis hver af de to begreber indeholder den samme faktor, kan du kombinere de faktorer sammen.
- Dette giver os (x + 3) (x 2 - 6).
- 5Finde løsningen ved at kigge på rødderne. Hvis du har en x 2 i dine rødder, så husk, at både negative og positive tal opfylde denne ligning.
- Løsningerne er 3, og √ 6..
Del 2: factoring ved hjælp af gratis sigt
- 1Omarrangere udtrykket, så det er i form af ax 3 + bx 2 + cx + d.
- Lad os sige, at vi arbejder med ligningen: x 3 - 4x 2 - 7x + 10 = 0.
- 2Find alle de faktorer af "d". Den konstante "d" vil være det antal, der ikke har nogen variabler, såsom "x" ved siden af.
- Faktorer er de tal, du kan formere sammen for at få et andet nummer. I vores tilfælde er de faktorer på 10, eller "d",: 1, 2, 5 og 10.
- 3Find en faktor, der forårsager polynomium til lige nul. Vi ønsker at bestemme hvilken faktor gør polynomiet lig nul, når vi erstatte faktor for hver "x" i ligningen.
- Lad os starte med at bruge vores første faktor, 1.. Lad os erstatte "1" for hver "x" i ligningen:
(1) 3 - 4 (1) 2 - 7 (1) + 10 = 0 - Det giver os: 1 - 4-7 + 10 = 0.
- Fordi 0 = 0 er et sandt udsagn, ved vi, at x = 1 er en løsning.
- Lad os starte med at bruge vores første faktor, 1.. Lad os erstatte "1" for hver "x" i ligningen:
- 4Gøre lidt omarrangere. Hvis x = 1, kan vi omarrangere redegørelsen at se lidt anderledes uden at ændre, hvad det betyder.
- "X = 1" er det samme som "x - 1 = 0" eller "(x - 1)". Vi har netop trukket et "1" fra hver side af ligningen.
- 5Faktor din root ud af resten af ligningen. "(X - 1)" er vores rod. Lad os se om vi kan faktor ud af resten af ligningen. Lad os tage det en polynomiel ad gangen.
- Kan vi faktor (x - 1) ud af x 3? Nej, vi kan ikke. Være kan vi låne en-x 2 fra den anden variabel, så kan vi faktor det: x 2 (x - 1) = x 3 - x 2.
- Kan vi faktor (x - 1) ud af hvad der er tilbage fra vores anden variabel? Nej, igen kan vi ikke. Vi har brug for at låne en anden lille smule fra den tredje variabel. Vi er nødt til at låne en 3x from-7x. Det giver os-3x (x - 1) =-3x 2 + 3x.
- Da vi tog en 3x from-7x, vores tredje variabel er nu-10x og vores konstante er 10. Kan vi faktor dette? Vi kan! -10 (X - 1) =-10x + 10.
- Hvad vi gjorde var omarrangere de variabler, så vi kunne medregne en (x - 1) ud af hele ligningen. Vores omarrangeret ligning ser sådan ud: x 3 - x 2 - 3x 2 + 3x - 10x + 10 = 0, men det er stadig det samme som x 3 - 4x 2 - 7x + 10 = 0.
- 6Fortsæt med at erstatte de faktorer i den frie sigt. Kig på de tal, vi indregnet ud ved hjælp af (x - 1) i trin 5:
- x 2 (x - 1) - 3x (x - 1) - 10 (x - 1) = 0. Vi kan omarrangere dette at være meget nemmere at faktor en gang mere: (x - 1) (x 2 - 3x - 10) = 0.
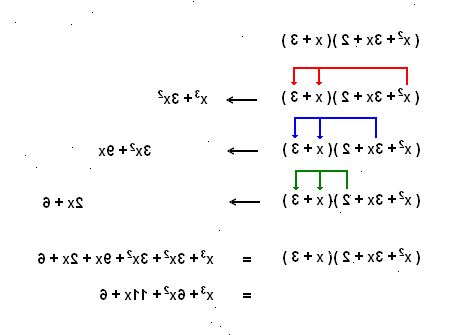
- Vi forsøger blot at faktoren (x 2 - 3x - 10) her. Dette faktorer ned i (x + 2) (x - 5).
- 7Dine løsninger vil være de multipliceret rødder. Du kan kontrollere, om dine løsninger faktisk virker ved at tilslutte hver enkelt individuelt, tilbage i den oprindelige ligning.
- (X - 1) (x + 2) (x - 5) = 0 Dette giver os opløsninger af 1, -2, og 5.
- Plug -2 tilbage i ligningen: (-2) 3. - 4 (-2) 2-7 (-2) + 10 = -8 - 16 + 14 + 10 = 0.
- Stik 5 tilbage ind i ligningen: (5) 3 - 4 (5) 2-7 (5) + 10 = 125 - 100 - 35 + 10 = 0.
Tips
- Den kubiske polynomium er et produkt af tre første grads polynomier eller et produkt på en første-gradspolynomiet og en anden unfactorable andengradspolynomiet. I dette sidste tilfælde bruger vi lang division efter at finde den første grad polynomium for at få den andengradspolynomiet.
- Der er ingen unfactorable kubiske polynomier mere end de reelle tal, fordi hver kubikmeter skal have en reel rod. Cubics såsom x ^ 3 + x + 1, der har en irrationel real rod kan ikke blive en faktor i polynomier med heltal eller rationelle koefficienter. Selv om det kan være en faktor med den kubiske formel, er det irreducible som et heltal polynomium.
