Determinanter for matricer er meget nyttige og nødvendige for at finde den inverse af en matrix ved hånden samt for anvendelsen af visse ligning løse processer såsom Cramers regel. Også, hvis determinanten er 0, du kender de ligninger, som udgør din matrix er lineært afhængige.
Steps
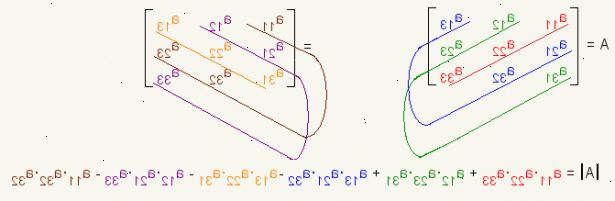
- 1Lad M være 3x3 matrix og dens determinant vil være | m |.
Eksempel:en 11 en 12 en 13 1 5 3 M = en 21 en 22 en 23 = 2 4 7 en 31 en 32 en 33 4 6 2 - 2Tag en reference række eller kolonne. Tager en reference række eller kolonne i dette problem er et afgørende skridt, som hvis du vælger klogt, så kan du lette problemet meget og løse problemet i meget kortere tid.
- Generelt første række er taget som reference. Hvis den givne matrix har nul i dens elementer, og vælg derefter henvisningen række eller kolonne, der har de fleste nuller.
- Der er et skilt konvention til reference række eller kolonne, hvorefter du er nødt til at gøre beregningen. Bemærk, at denne tegnkonvention kun til reference række eller kolonne. Tegnet konvention er angivet nedenfor.
(+) A 11 (-) A 12 (+) En 13 M = (-) A 21 (+) A 22 (-) A 23 (+) A 31 (-) 32 (+) En 33
- Generelt første række er taget som reference. Hvis den givne matrix har nul i dens elementer, og vælg derefter henvisningen række eller kolonne, der har de fleste nuller.
- 3Vælg det første element fra henvisningen række eller kolonne, og krydser ud af andre elementer fra række og kolonne, det valgte element er in.
- Beregn determinanten af 2X2 matrix, som er tilbage efter overstregning elementer i ovenstående trin. Multiplicerer 2X2 determinant med udvalgte henvisning element og tilsvarende tegn for, at der henvises element.
- Hvis du tager første række som reference, så for det første element:
(+) A 11 * ((a 22 * a 33) - (a 23 * 32)) = 1 (4 * 2-7 * 6) = -34
- Beregn determinanten af 2X2 matrix, som er tilbage efter overstregning elementer i ovenstående trin. Multiplicerer 2X2 determinant med udvalgte henvisning element og tilsvarende tegn for, at der henvises element.
- 4Vælg det andet element fra henvisningen række eller kolonne, og krydser ud af andre elementer fra række og kolonne, det valgte element er in.
- Beregn determinanten af 2X2 matrix, som er tilbage efter overstregning elementer i ovenstående trin. Multiplicerer 2X2 determinant med udvalgte henvisning element og tilsvarende tegn for, at der henvises element.
- Hvis du tager første række som reference, så for det andet element:
(-) A 12 * ((a 21 * a 33) - (a 23 * a 31)) = (-) 5 (2 * 2-7 * 4) = 120
- Beregn determinanten af 2X2 matrix, som er tilbage efter overstregning elementer i ovenstående trin. Multiplicerer 2X2 determinant med udvalgte henvisning element og tilsvarende tegn for, at der henvises element.
- 5Vælg det tredje element fra henvisningen række eller kolonne, og krydser ud af andre elementer fra række og kolonne, det valgte element er in.
- Beregn determinanten af 2X2 matrix, som er tilbage efter overstregning elementer i ovenstående trin. Multiplicerer 2X2 determinant med udvalgte henvisning element og tilsvarende tegn for, at der henvises element.
- Hvis du tager første række som reference, så for det tredje element:
(+) A 13 * ((a 21 * 32) - (a 22 * a 31)) = 3 (2 * 6 - 4 * 4) = -12
- Beregn determinanten af 2X2 matrix, som er tilbage efter overstregning elementer i ovenstående trin. Multiplicerer 2X2 determinant med udvalgte henvisning element og tilsvarende tegn for, at der henvises element.
- 6Tilføj resultaterne for tre elementer kommissorium række eller kolonne for at få bestemmende for denne 3x3 matrix.
| M | = -34 + 120-12 = 74
Tips
- Hvis alle elementer i en række eller kolonne i en matrix er lig nul, så bestemmende for denne artikel er også nul.
- Hvis du tager første række som reference, så afgørende vil være:
| M | = a 11 * ((a 22 * a 33) - (a 23 * 32)) - en 12 * ((a 21 * a 33) - (a 23 * a 31)) + a 13 * ( (a 21 * 32) - (a 22 * a 31)) - Denne metode omfatter kvadratiske matricer af enhver størrelse.
Advarsler
- Prøv at undgå at gøre determinanter for noget større end en 3x3 med hånden.
