Syntetisk division er en metode til afsnit, hvor du udfører division på de koefficienter, fjerne variabler og eksponenter. Det giver dig mulighed for at tilføje hele processen snarere end trække (lang division).
Steps
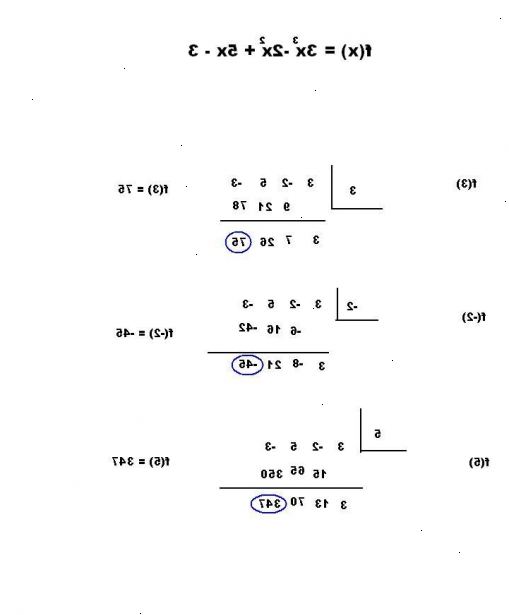
- 1Ved anvendelsen af denne artikel
(X 3 + 2 x 2 - 4 x + 8) ÷ (x + 2)
er et eksempel for alle trin. - 2Vende tegn på konstant i divisor
(X + 2) er divisor. De to bliver negativ. - 3Placer denne nye nummer af sig selv og placere en "baglæns l" på sin højre side
-2 |
- 4Til højre for denne, alt af koefficienterne skriver (i standard form)
-2 | 1 2 -4 8
- 5Nedbringe første koefficient
-2 | 1 2 -4 8
1
- 6Gang dette med den nye divisor og placere den under den anden koefficient
-2 | 1 2 -4 8
-2
- 7Kombiner den anden koefficient, og produktet
-2 | 1 2 -4 8
-2
- 8Gang dette beløb med den nye divisor og sted, under den tredje koefficient
-2 | 1 2 -4 8
-2 0
- 9Kombiner disse
-2 | 1 2 -4 8
-2 0
- 10Fortsæt på samme måde, indtil du har fundet den endelige sum. Denne sum er den resterende
-2 | 1 2 -4 8
-2 0 8
1 0 -4 | 16 - 11Hvis du vil skrive svaret, placere hver af de beløb, ved siden af en variabel i en mindre effekt end den oprindelige det er linet op med. I dette tilfælde er den første sum placeret ved siden af en x opløftet til anden potens (én mindre end tre), den anden sum er nul, så det er ikke en del af svaret, og den negative fire er ikke ud for en x
-2 | 1 2 -4 8
-2 0 8
1 0 -4 | 16
x 2 + 0 x - 4 R 16
x 2 - 4 R16 - 12Her endelig konkluderer vi, at når (x 3 + 2 x 2 - 4 x + 8) er divideret med (x + 2), kvotienten er (x 2 - 4), og resten er 16.. Hvis der i nogle tilfælde resten er 0, den oprindelige divisor var en faktor af polynomiet.
Tips
- For at kontrollere dit svar, multipliceres kvotienten ved divisor og tilsæt resten. Det bør være den samme som den oprindelige polynomium.
- (Divisor) (kvotient) + (resten)
- (X + 2) (x 2 - 4) + 16
- Brug FOIL metode, formere sig.
- (X 3 - 4 x + 2 x 2-8) + 16
- x 3 + 2 x 2 - 4 x - 8 + 16
- x 3 + 2 x 2 - 4 x + 8
