En regulær polygon er en 2-dimensional konveks figur bestående af kongruente sider og vinkler lige i foranstaltning. En konveks figur er en figur med vinkler mindre end eller lig med 180 grader.
Denne artikel omhandler, hvordan du finder området for regulære polygoner med mere end fire sider. Hvis du ønsker at vide arealet af en firkant, go. Hvis du ønsker at vide, hvordan man finder arealet af en trekant, kan du gå
Steps
- 1Arealet af nogen regelmæssig polygon er givet ved formlen:
Area = (AXP) / 2,
hvor a er længden af apothem og p a> er omkredsen af polygonen.
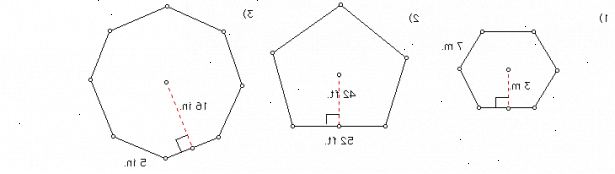
Apothem er liniesegmentet fra midten af en regulær polygon til midten af en side. Kanten kan findes ved at multiplicere sidelængde med antallet af sider i polygonen. - 2Sammen med sidelængden, hvis længden af apothem også direkte gives derefter finde området for en sådan en polygon er ikke mere end en kage gåtur. Sæt blot værdierne af a og p a> i formlen og få området.
For eksempel overveje at finde arealet af en regulær sekskant (6 sider) i sidelængde 10 enheder og apothem måling 5sqrt (3) enheder. - 3Sammen med sidelængden, så hvis længden af apothem ikke er direkte givet det kan beregnes efter følgende formel:
a = (s / 2) x barneseng (180 0 / n),
hvor a er længden af apothem, s a> er sidelængden, og n er antallet af sider i polygonen.- Som et eksempel overveje at finde arealet af en regulær nonagon (9 sider) af side-længde 5 enheder.
- Find apothem
- Find omkredsen
- Find området ved hjælp af formlen nævnt i trin 1 ovenfor.
- Som et eksempel overveje at finde arealet af en regulær nonagon (9 sider) af side-længde 5 enheder.
Tips
- For mere information om at arbejde med kvadratrødder, så tjek de artikler Sådan formere kvadratrødder og hvordan man opdele kvadratrødder.
Advarsler
- Hvis tegningen på din ottekant (eller hvad) er blevet adskilt i trekanter, og en trekant areal er mærket, så du ikke behøver at gøre det hele apothem business. Bare tage det område, at én trekant, og ganges med det antal sider i den oprindelige polygon.
