Sådan faktor andengrads polynomier (kvadratiske ligninger)

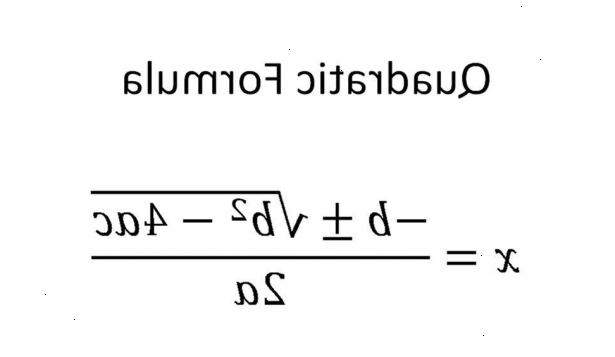
1. 1
   Opsæt dit udtryk. Bestil tallene fra højeste til laveste strømforbrug, og derefter faktor ud den største fælles faktor, hvis en sådan findes.
   6 + 6x ² + 13x
   6x ² + 13x + 6
2. 2
   Find indregnet form, ved hjælp af en af nedenstående metoder.
   (2x + 3) (3x + 2)
   
3. 3
   Tjek dit arbejde ved at multiplicere de faktorer, hjælp folie. Derefter kombinere lignende vilkår, og du er færdig!
   (2x + 3) (3x + 2)
   6x ² + 4x + 9x + 6
   6x ² + 13x + 6
   

Trial and error metoden

Hvis du har en forholdsvis simpel polynomium, vil du være i stand til at finde ud af de faktorer selv. BEMÆRK: Med denne metode kan ikke være så simpelt som når factoring mere komplicerede trinomials.

Eksempel: 3x ² + 2x - 8

1. 1
   Opregne de faktorer i en sigt og c sigt.
   a = 3 faktorer: 1 og 3
   c = -8 faktorer: 2 og 4 eller 1 og 8.
   
2. 2
   Skriv ned to sæt parenteser med tomme rum som dette:
   (X) (x)
   
3. 3
   Fylde rum foran x'er med et par mulige faktorer af en værdi. Der er kun én mulighed for vores eksempel:
   ( 3x) ​​( 13x) (x)
   
4. 4
   Udfylde de to rum efter x'er med et par faktorer for den konstante. Lad os sige, vi vælger (3x 8) (x 18) (x).
   
5. 5
   Beslut hvilke tegn skal være mellem x'erne og tallene. Her er en guide:
   Hvis ax ² + bx + c derefter (x + h) (x + k)
   Hvis ax ² - bx - c eller ax ² + bx - c derefter (x - h) (x + k)
   Hvis ax ² - bx + c derefter (x - h) (x - k)
   For vores eksempel 3x ² + 2x - 8, så (x - h) (x + k)
   Vi bliver nødt til at gætte som for resten. (3x + 8) (x - 1)
   
6. 6
   Test dit valg ved at multiplicere (brug FOIL) de to parenteser sammen. Hvis den midterste sigt ikke er mindst den korrekte værdi (der ses bort fra positiv eller negativ), du har valgt de forkerte c faktorer.
   (3x + 8) (x - 1)
   3x ² - 3x + 8x - 8
   3x ² + 5x - 8 ≠ 3x ² + 2x - 8
   
7. 7
   Swap ud af dine valg, hvis det er nødvendigt. I vores eksempel, lad os prøve 2 og 4 i stedet for 1 og 8: (3x + 2) (x - 4)
   
   • Nu er vores c sigt er en -8.
   • Men vores Udenfor / Inside combo er-12x og 2x, som ikke vil kombinere for at gøre det rigtige b løbetid +2 x.
8. 8
   Omvendt rækkefølge, hvis nødvendigt. Lad os prøve at flytte 2 og 4 omkring: (3x + 4) (x - 2)
   
   • c sigt er stadig okay.
   • Udenfor / Inside combo is-6x og 4x. Hvis vi kombinerer dem, får vi temmelig tæt på 2x vi sigter efter --- rigtige mængde, forkert tegn.
9. 9
   Dobbelttjek dit tegn, hvis nødvendigt. Vi kommer til at holde fast i den samme rækkefølge, men swap som man har subtraktion: (3x - 4) (x + 2)
   
   • c sigt er stadig okay.
   • Udenfor / Inside combo er nu 6x og-4x. Dette vil kombinere til at skabe den positive 2x fra det oprindelige problem, så disse er de korrekte faktorer.

Nedbrydning metode

Hvis tallene er store eller er du bare træt af at gætterier bruge denne metode.

Eksempel: 6x ² + 13x + 6

1. 1
   Multiplicer et begreb (6 i eksemplet) med c sigt (også 6 i eksemplet).
   6 • 6 = 36
   
2. 2
   Find to tal, når ganget lige dette nummer (36) og tilføje op til at være den b sigt (13).
   4 • 9 = 36 4 + 9 = 13
   
3. 3
   Stedfortræder de to tal, du kommer ind i denne form, som k og h (Rækkefølgen betyder ikke noget): ax ² + kx + hx + c
   6x ² + 4x + 9x + 6
   
4. 4
   Faktor polynomiet ved gruppering. Organiser ligningen, så du kan tegne den største fælles faktor af de første to begreber, og de sidste to valgperioder. Begge multipliceret grupper bør være den samme. Tilsæt GCF s sammen og vedlægge dem i parentes ved siden af ​​indregnet gruppen.
   6x ² + 4x + 9x + 6
   2x (3x + 2) + 3 (3x + 2)
   (2x + 3) (3x + 2)
   

Triple play metode

Det er meget lig den nedbrydning metode, men det er enklere.

Eksempel: 8x ² + 10x + 2

1. 1
   Multiplicer et begreb (8 i eksemplet) med c sigt (2 i dette eksempel).
   8 • 2 = 16
   
2. 2
   Find de to tal, hvis produkt er dette tal (16) og hvis sum er lig med b sigt (10).
   2 • 8 = 16 8 + 2 = 10
   
3. 3
   Tag disse to tal (som vi vil kalde h og k), og erstatte dem i dette udtryk:
   (Ax + h) (ax + k)
   a
   (8x + 8) (8x + 2)
   8
   
4. 4
   Look at se, hvilken en af de to parenteser vilkår i tælleren er deleligt med en {i dette eksempel er det (8x + 8)}. Divider dette udtryk med en og efterlade den anden som er.
   (8x + 8) (8x + 2)
   8
   Svar: (x + 1) (8x + 2)
   
5. 5
   Tag GCF (hvis nogen) ud af et eller begge parenteser.
   (X + 1) (8x + 2)
   2 (x + 1) (4x + 1)
   

Forskel på to pladser

1. 1
   Faktor en GCF, hvis du har brug for.
   27x ^2-12
   3 (9x ² - 4)
   
2. 2
   Beslutte, om din ligning er en forskel på kvadrater. Den skal have to vilkår, og du bør være i stand til at tage kvadratroden af ​​vilkårene jævnt.
   √ (9x ²⁾ = 3x og √ (4) = 2 (bemærk, at vi har udeladt det negative fortegn)
   
3. 3
   Sæt A og C værdier fra din ligning ind i dette udtryk:
   (√ (a) + √ (c)) (√ (a) - √ (c))
   3 [(√ (9x ²⁾ + √ (4)) (√ (9x ²⁾ - √ (4))]
   3 [(3x + 2) (3x - 2)]
   

Brug den kvadratiske formel

Hvis alt andet fejler, og ligningen vil ikke faktor jævnt bruge den kvadratiske formel.
Eksempel: x ² + 4x + 1

1. 1
   Sæt de tilsvarende værdier i den kvadratiske formel:
   x =-b ± √ (b ² - 4ac)
   2a
   x = -4 ± √ ^(april 02-04 • 1 • 1)
   2 • 1
   
2. 2
   Løs for x. Du bør få to x-værdier.
   x = -4 ± √ (16 - 4)
   2
   x = -4 ± √ (12)
   2
   x = -4 ± √ (4 • 3)
   2
   x = -4 ± 2 √ (3)
   2
   x = -2 ± √ (3)
   x = -2 + √ (3) eller x = -2 - √ (3)
   
3. 3
   Sæt x-værdierne (h og k) i dette udtryk: (x - h) (x - k)
   (X - (-2 + √ (3)) (x - (-2 - √ (3))
   (X + 2 + √ (3)) (x + 2 - √ (3))
   

Ved hjælp af en regnemaskine

Disse retninger er for en TI grafregneren. Dette er især anvendeligt i standardiserede prøver.

1. 1
   Indtast din ligning i [y =] skærm.
   y = x ² - x - 2
   
2. 2
   Tryk på [Graph]. Du bør se en jævn bue.
   
3. 3
   Lokalisere, hvor lysbuen skærer x-aksen. Disse er x-værdierne.
   (-1, 0), (2, 0)
   x = -1, x = 2
   
   • Hvis du ikke kan identificere dem ved synet tryk på [2nd] og derefter [TRACE]. Tryk på [2], eller vælg "nul". Skub markøren til venstre for et krydsfelt, og tryk på [ENTER]. Skub markøren til højre for en skærer, og tryk på [ENTER]. Skub markøren så tæt som muligt på den skærer og tryk [ENTER]. Lommeregneren vil finde x-værdi. Gør dette for den anden skærer også.
4. 4
   Sæt x-værdierne (h og k) i dette udtryk: (x - h) (x - k)
   (X - (-1)) (x - 2)
   (X + 1) (x + (-2)) stort plus føje den til fælles faktor