Hvordan at tilføje eller trække vektorer

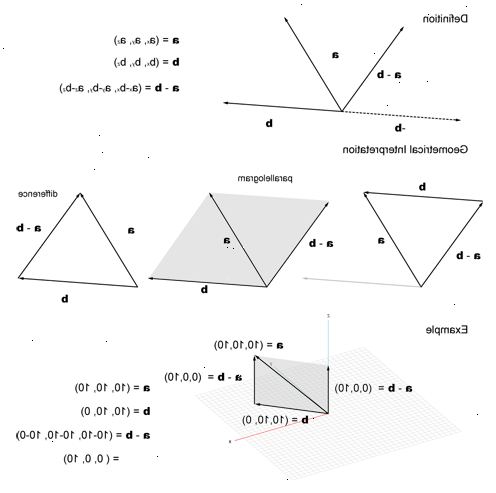
Vector addition eller subtraktion trin

1. 1
   Hvis vi har 2 vektorer, vektor A og vektor b,
   • A = <a1,b1,c1>
   • B = <a2,b2,c2>
2. 2
   Hvis vi ønsker at tilføje vektor A til vektor b, og derefter
   • A + b = <a1+a2,b1+b2,c1+c2>
3. 3
   Hvis vi ønsker at trække vektor A fra vektor b, og derefter
   • Ab = <a1-a2,b1-b2,c1-c2>

Metode én: hoved til hale

1. 1
   Tag en vektor, og identificere dens hoved og dens hale. Du kan lave en skala tegning eller en grov skitse. Hvis du laver en skala tegning, skal du passe på konstruere alle vinkler meget nøje.
2. 2
   Skub anden vektor, så halen slutter til den første hoved
3. 3
   Deltag alle andre vektorer efterfølgende. Ordren betyder ikke noget overhovedet, og denne metode kan bruges til et vilkårligt antal vektorer. De bør dog være orienteret således, at de begynder at danne en polygon.
4. 4
   Deltag i halen af den første vektor til lederen af det sidste. Dette er den resulterende vektor, eller summen af alle dine vektorer.
   • Hvis du var at tegne diagrammet til en skala, tegning alle vinkler nøje, kan du måle længden af ​​den resulterende vektor ved hjælp af en lineal. Også derefter måle vinklen at det resulterende gør med enten en bestemt vektor, eller den vandrette / lodrette osv.
   • Hvis du lavede en skitse, bliver du nødt til at beregne størrelsen af ​​den resulterende bruge trigonometri. Du kan finde og hjælpsomme her. Hvis du tilføjer mere end to vektorer sammen, er det nyttigt først at tilføje to og derefter bruge den resulterende med den tredje vektor, og så videre.
5. 5
   Repræsentere dine resulterende vektor. For eksempel, hvis vektorerne repræsenterede hastigheder så skriv "En hastighed x ms ^-1 ved y ^o til den vandrette / lodrette / etc".

Metode to: vinkelrette komponenter

Denne metode er normalt anvendes i den kartesiske plan, men kan anvendes til andre vektorer også.

1. 1
   Split hver vektor i to vinkelrette komponenter. For eksempel opdele hver vektor i sine horisontale og vertikale komponenter. Det er almindeligt at opdele vektorer i komponenter langs x-og y-akser i kartesiske plan. Enhedsvektoren langs x-aksen konventionelt skrives som jeg, at langs y-aksen som j.
   • For at løse en kraft i komponenter, bliver du nødt til at vide den vinkel, at det gør med det vandrette, lodrette, x-aksen eller y-aksen. Når denne vinkel er kendt, kan du konstruere en retvinklet trekant med den kraft som hypotenusen og de to andre sider langs x-og y-aksen. Længderne af de to andre sider er omfanget af komponenterne langs disse retninger, og kan beregnes ved hjælp trigonometri. Den side støder op til vinklen er xcos (vinkel), og den modsatte side er xsin (vinkel), hvor x er størrelsen af ​​den oprindelige kraft.
   • Hvis en komponent peger mod venstre eller nedad, er det givet et negativt fortegn (-).
2. 2
   Tilføj alle størrelserne af de horisontale komponenter (eller dem langs x-aksen) sammen. Separat tilsættes alle størrelserne af de lodrette komponenter (eller dem langs y-aksen). Hvis en komponent har et negativt fortegn (-), er dens størrelse subtraheres, snarere end tilsat.
3. 3
   Beregn størrelsen af den resulterende hjælp af Pythagoras 'sætning. Sætningen kan anføres: c ² = a ² + b ^2, hvor c er størrelsen af den resulterende vektor, en er størrelsen af summen af komponenterne langs x-aksen, og b er størrelsen af summen af komponenterne langs y-aksen.
4. 4
   Beregne den vinkel, den resulterende danner med vandret (eller x-aksen). Bruge formlen θ = tan ^-1 (b / a), hvor θ er vinklen at det resulterende danner med x-aksen eller den vandrette.
5. 5
   Repræsentere dine resulterende vektor.
   • For eksempel, hvis vektorerne repræsenterede kræfter så skriv "En kraft x N ved y ^o med vandret / x-aksen / etc".

Metode tre: vector subtraktion

1. 1
   Trække ved at tilføje en negativ. Subtrahere en vektor fra en anden kan ses som at tilføje sin "negativ".
2. 2
   Find den negative af vektoren. Dette er den samme i størrelsesorden til den oprindelige vektor, men modsat i retning. Du kan repræsentere det ved at gøre den oprindelige vektor, men tegning pilen den anden vej rundt, således at halen bliver hoved og hovedet bliver halen.
3. 3
   Følg en tilsætning ovennævnte fremgangsmåde, ved hjælp af negative. Brug en af ​​de to tilsætning beskrevet ovenfor for at tilføje "negativ" af vektoren, der skal trækkes og vektoren måtte trækkes fra.