Sådan finder overfladearealet af prismer

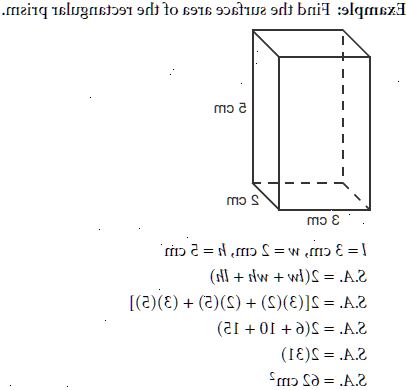
1. 1
   Label så mange sider, som du kan. Det gode ved prismer er, at de matchende ende par gør det nemt at bestemme en masse af de enkelte målinger uden at skulle løse for noget. Målinger, der er givet for et af endeformer (ex. højde af trekanten, radius af en cirkel) gælder også for tilsvarende facon i den anden ende. Desuden, hvis du kender længden af ​​den ene side af prisme, du kender længden af ​​alle siderne. Fordel disse numre som nødvendigt omkring dit prisme at se, hvad du har at arbejde med.

Find arealet af en af ​​de matchende ender

1. 1
   Hvis de matchende ender er trekanter, find arealet af en trekant bruger.
2. 2
   Hvis de matchende ender er kvadratisk eller rektangulær, formere base ved højden. Basen og højde er simpelthen målingerne af to vinkelrette sider af kvadrat eller et rektangel, en firkant, er denne to målinger samme. Du skal blot formere begge tal sammen for at finde det område af enden.
3. 3
   Hvis de matchende ender er cirkler, formere pi ved hjælp af radius potens. Radius er længden fra cirklens centrum til yderkanten. Square Dette tal (dvs. ganges med sig selv), og derefter multipliceres resultatet med pi (3.14159...). Dette giver dig det område af enden.
   • Hvis du har fået diameter (dvs. længden på tværs af hele cirklen), dividere dette tal i halvdelen at finde radius.
   • Hvis du har fået omkredsen (dvs. længden af den udvendige kant af cirklen), dividere dette tal med pi og dividere dette resultat med 2 for at finde radius.
4. 4
   Hvis tilsvarende ender er parallelogrammer, formere base ved højden. Parallelogrammer er skrå firkanter (som åbne kasser, der er blevet skubbet til den ene side), de har to par af parallelle sider, men ingen af ​​hjørnerne er rette vinkler. Bunden af et parallelogram er simpelthen længden af en af de to lange, forskudte sider; højden, dog er afstanden mellem disse to sider, ikke længden af en af de vinklede sider. Hvis denne højde ikke allerede er givet til dig, vil problemet bede dig om at løse for det ved at dreje på de vinklede sider i en retvinklet trekant og giver dig længden af ​​to af siderne af trekanten. Til at løse for højden på denne måde:
   • Brug Pythagoras 'læresætning, som er A ^ 2 + b ^ 2 = c ^ 2. Hypotenusen af trekanten, eller C, er simpelthen den side af trekanten modsat den rette vinkel. Vi ringer på den anden side, der er blevet givet B C,>. For at løse for højden, som vi vil kalde A, omarrangere formel A ^ 2 = C ^ 2 - B ^ 2. Multiplicer C ved selv, derefter multiplicere B af sig selv. Fratræk andet resultat fra den første til at få A ^ 2, for derefter at løse for A, finder kvadratroden af ​​dette beløb. Dette er højden af ​​parallelogram, som du kan nu formere ved basen for at finde det samlede areal.
5. 5
   Hvis tilsvarende ender er en anden polygon, bryde formen ned i trekanter at løse. En pentagon, for eksempel, kan opdeles i 5 lige store trekanter, en sekskant kan opdeles i 6, og så videre. Når du er færdig med at tegne trekanter, løse for arealet af en trekant bruger. Når du er færdig, formere sig, at området med det samlede antal af lige trekanter, du har tegnet.
   • Hvis polygon ikke kan opdeles i perfekt trekanter, bryde det ned i trekanter og firkanter. Find det område, hver figur individuelt med formen guider ovenfor, og derefter tilføje dem sammen for at finde det samlede areal af polygonen.
6. 6
   Bemærk det område herpå på dit papir og overlade det alene for nu. Du vil komme tilbage til det senere.

Find omkredsen af ​​en af ​​de matchende ender

1. 1
   Løs for eventuelle manglende sider. Efter løsning for området, kan du allerede kender længden på hver side af formen i slutningen af ​​dit prisme. Hvis ikke, løse ved hjælp af en af ​​følgende metoder:
   • Hvis de matchende ender er trekanter, løse for alle sider ved hjælp af Pythagoras 'læresætning. Pythagoras 'læresætning er A ^ 2 + b ^ 2 = c ^ 2: A og B er basen og højden af en retvinklet trekant, og C er hypotenusen, som er simpelthen den side modsat den rette vinkel.
     • Hvis du har fået A og B, bruge formlen C ^ 2 = A ^ 2 + B ^ 2. Multiplicer A af sig selv, formere B af sig selv, og tilsæt de to tal sammen, hvilket giver dig C ^ 2. For derefter at løse for C, bare finde kvadratroden af ​​dette beløb.
     • Hvis du har fået C og B: bruge formlen A ^ 2 = C ^ 2 - B ^ 2. Multiplicer C af sig selv, formere B af sig selv, og trække det andet resultat fra den første, hvilket giver dig A ^ 2. For derefter at løse for A, skal du blot finde kvadratroden af ​​dette beløb.
     • Hvis du har fået C og A: bruge formlen B ^ 2 = C ^ 2 - A ^ 2. Multiplicer C af sig selv, multipliceres A af sig selv, og trække det andet resultat fra den første, hvilket giver dig B ^ 2. For derefter at løse for B, bare finde kvadratroden af ​​dette beløb.
   • Hvis tilsvarende ender er cirkler, finde omkredsen. Formlen for omkreds er C = D x pi: C er omkreds og D er diameteren. Hvis du har radius, blot multipliceres med 2 for at finde diameteren.
   • Hvis de matchende ender er endnu polygon, bryde formen ned i trekanter og / eller kvadrater som før og finde de udvendige kanter ved at løse for disse figurer individuelt. Brug formen guider ovenfor, hvis det er nødvendigt.
2. 2
   Markér perimeter målinger på dit papir. Du kan derefter bruge dem til at bestemme det område siderne af parallelogram.

Find arealet af hver side

1. 1
   Bemærk længden af prisme. Dette er afstanden mellem de to matchende ender af prisme. Da enderne af prisme er parallelle, vil denne afstand være ensartet i hele - også selvom de matchende ender er begge vinklet. Det betyder, at hvis du kender længden af ​​den ene side, du kender længden af ​​alle siderne.
2. 2
   Find arealet af hver side. Hver side vil enten være en firkant / rektangel eller et parallelogram. Parallelogrammer er skrå firkanter (som åbne kasser, der er blevet skubbet til den ene side), de har to par af parallelle sider, men ingen af ​​hjørnerne er rette vinkler.
   • For at finde arealet af et kvadrat / rektangel, formere base ved højden. Basen og højde er simpelthen målingerne af to vinkelrette sider af kvadrat eller et rektangel, en firkant, er denne to målinger samme. Du skal blot formere begge tal sammen for at finde det område af enden.
   • At finde arealet af et parallelogram, formere base ved højden. Bemærk, at bunden af et parallelogram er simpelthen længden af en af de to lange, forskudte sider; højden, dog er afstanden mellem disse to sider, ikke længden af den ene af de vinklede sider. Hvis du kun kender længden af ​​den skrå side, men ikke parallelogram sande højde, tegne en linje gennem hver side af parallelogram, gøre det til en perfekt kvadrat / rektangel med en trekant på hver ende. For at finde højden ved hjælp af denne trekant:
     • Brug Pythagoras 'læresætning, som er A ^ 2 + b ^ 2 = c ^ 2. Hypotenusen af trekanten, eller C, er simpelthen den side af trekanten modsat den rette vinkel. Vi ringer på den anden side, der er blevet givet B C,>. For at løse for højden, som vi vil kalde A, omarrangere formel A ^ 2 = C ^ 2 - B ^ 2. Multiplicer C ved selv, derefter multiplicere B af sig selv. Fratræk andet resultat fra den første til at få A ^ 2, for derefter at løse for A, finder kvadratroden af ​​dette beløb. Dette er højden af ​​parallelogram, som du kan nu formere ved basen for at finde det samlede areal.
   • Hvis prisme er cylindrisk, finde det område af siderne ved at multiplicere omkreds, som du har løst i det foregående afsnit, med det samlede højde. (Billede cylinderen har et stykke papir viklet rundt, som, når uindpakkede, danner en perfekt kvadrat eller rektangel. Omkredsen kan derefter opfattes som længden af ​​det stykke stykke papir, som kan løses som enhver pladsen ved multiplicere længde gange højde.)

Find det samlede areal

1. 1
   Multiplicer området af enden af prisme med 2. Find det nummer, du markerede ned, når du har løst for området med en af ​​de matchende ender og fordoble det til at redegøre for den anden ende.
2. 2
   Læg de områder af siderne af prismet. Hvis din prisme har trekantede ender, vil du blive tilføje op tre sider, og hvis de er femkantet, vil du blive tilføjet fem sider; osv. Hvis prisme er cylindrisk, behøver du ikke at tilføje noget, da der kun er én "side ".
3. 3
   Tilføj det samlede areal af enderne til det samlede areal af siderne. Dette giver dig det samlede areal af prisme.