Algebra er et meget vigtigt redskab i hverdagen, og kan hjælpe dig med at løse dag-til-dag problemer. Uanset om du er helt ny på dette koncept eller bare brug for en lille gennemgang, denne vejledning er sikker på at hjælpe.
Steps
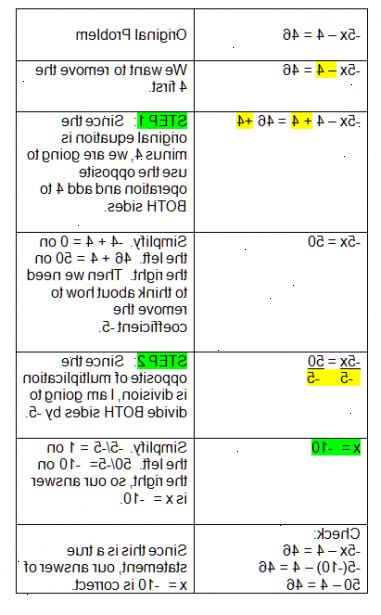
Løsning totrins ligninger med kun én variabel
- 1Denne proces er lettere, hvis du følger en demonstration. Vi vil bruge eksemplet problemet vist her:-4x + 7 = 15
- 2Få den variable udtryk af sig selv. Den variable sigt er bogstavet og uanset koefficient er foran den. I vores tilfælde, at vi adskille-4x ved fra +7. Dette kaldes additiv invers. Vi gør dette ved at vende driften af 7.. I dette eksempel anvendes 7 bliver tilføjet, og derfor skal vi trække 7 fra venstre side af ligningen. For at holde den i balance, skal vi også trække 7 fra højre side:
- Forsigtig: uanset hvad du gør til den ene side af en ligning, skal du gøre til den anden side Dette er den gyldne regel for Algebra.. Derfor er 7 trækkes fra 15 samt. Vi behøver blot at trække 7 én gang pr side, hvilket er grunden til, at 7 er ikke trækkes fra-4x så godt.
- 3Bringe ned variabel sigt. Omskriv ligningen med additivet inverse handling udføres. Vores nye ligning er-4x = 8
- 4Eliminer variablens koefficient. "Koefficient" er den korrekte ord for tallet knyttet til variablen. I dette eksempel er den koefficient -4. Ligesom vi elimineret 7, så vi fjerner -4. Som det multiplicere med x, vi vende multiplikation og dividere hver side ved -4. Formlen for dette er -4 (x) ÷ -4 = 8 ÷ -4. -4.
- Igen skal uanset hvad du gør til ligningen skal gøres til begge sider. Det er derfor, du ser ÷ -4 to gange.
- 5Beregne resultatet. -4x ÷ -4 = x og 8 ÷ -4 = -2. Derfor x = -2
- 6Mærk svaret, hvis det er nødvendigt. Hvis ligningen var en del af en historie problem, for eksempel, kan vi ønsker at mærke det
Yderligere eksempler
- 1Nogle gange er du nødt til at flytte den konstante til venstre i stedet for til højre:
- I dette tilfælde, 11 = 3 - 7x. Trække 3 fra begge sider, så vores Ligningen bliver:
- 8 =-7x.
- Annullere de x ved at dividere det med 7. Udfør funktionen på begge sider:
- 8 ÷ -7 = x
- -8/7 = X
- -1.14 = X
- Bemærk: du kan også vende ligningen rundt: 3 - 7x = 11 -> x = 1,14
- I dette tilfælde, 11 = 3 - 7x. Trække 3 fra begge sider, så vores Ligningen bliver:
- 2Undertiden det sidste trin er at formere end kløften:
- I betragtning af de ligningen x / 5 + 7 = -3
- Fratræk 7 fra begge sider:
- (X / 5 + 7) - 7 = -3 - 7 eller x / 5 = -10
- Siden 5. er nævneren, formere i stedet for dividere hver side med 5 for at annullere 5 ud.
- (X / 5) * 5 = -10 * 5 eller x = -50
Løse ligninger med én variabel pr side
- 1Kontroller, at begge variabler bruger samme bogstav. Hvis de ikke gør det, så er denne metode vil ikke fungere.
- 2Flyt konstanterne på højre side ved hjælp af deres inverse. (Hvis det bliver tilføjet, skal du trække fra, og vice versa.
- I dette eksempel,-2x - 3 = 4x - 15. Annullere de tre:
- (-2x - 3) +3 = (4x - 15) +3 =-2x = 4x - 12
- 3Flyt de variabler til venstre side ved at tilføje deres inverse:
- -2x - 4x = (4x - 12) - 4x =-6x = -12
- 4Inddel ud koefficienten, hvis det er nødvendigt.
- -6x ÷ -6 = -12 ÷ -6
- x = 2
- 5Denne metode lægger vægt ender med variablen på venstre side. Det er ikke strengt nødvendigt. Men hvis du lige er startet ud med at løse ligninger, er det den anbefalede metode, da det ikke kræver selvstændig beslutningstagning.
Tips
- Hvis der ikke er noget nummer foran x, antage at det er en 1x
- Der kan ikke være et eksplicit konstant på hver side. Hvis der ikke er noget nummer efter et x, antage at det er x + 0
