Hvordan man beregner en kvadratrod med hånden

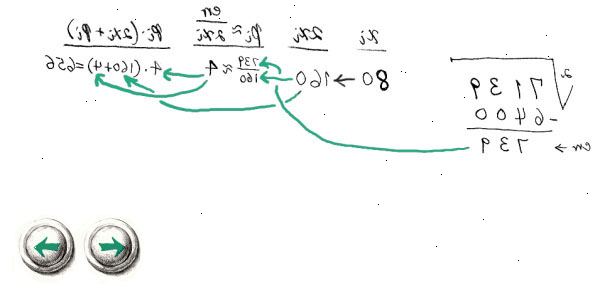
Beregning af en kvadratrod i hånden

1. 1
   Skriv nummeret ned, du ønsker at beregne kvadratroden af. Adskil cifrene i par, startende fra kommaet: 79,520,789,182.47897 bliver til "7 95 20 78 91 82 47 89 70".. Som et eksempel, så prøv at beregne kvadratroden af ​​780,14. Tegn to linjer som billedet viser og skrive "7 80. 14" til venstre. Øverst til højre, vil du have kvadratroden af ​​780,14.
   
2. 2
   Kig på den yderste venstre par og finde den største heltal n hvis pladsen er mindre end eller lig med den. Sted n i øverste højre kvadrant, og beregne kvadratet af n i nederste højre kvadrant. I denne artikel eksempel er, at parret 7.. Og 2 × 2 ≤ 7 <3 × 3, derfor n = 2. Skriv 2 i øverste højre kvadrant: det er det første ciffer af kvadratroden. Skriv 2 × 2 = 4 i nederste højre kvadrant, og du får brug for dette nummer i det næste trin.
   
3. 3
   Trække det nummer, du netop beregnet ud fra den yderste venstre par. For artiklens eksempel trække 4 fra parret "7", som giver dig 3.
   
4. 4
   Drop det næste par på venstre side. Gange antallet i øverste højre kvadrant med to og skrive det i nederste højre kvadrant, tilføjer "_ × _ =". I eksemplet er det næste par "80": skriv "80" ved siden af ​​3. Derefter to gange antallet øverst til højre er 4: write "4_ × _ =" i nederste højre kvadrant.
   
5. 5
   Find den største ciffer at erstatte understregningstegnene således at resultatet af multiplikationen er lavere end eller lig med den aktuelle nummer til venstre. I eksemplet gange 8, hvis du udskifter understregning med 8, 48, er 384, som er større end 380. Derfor 8 er for stor. Men 7 vil arbejde. Skriv 7 på understregninger og beregn: 47 gange 7 svarende til 329. Skriv 7 øverst til højre: Det er det andet ciffer i kvadratroden af ​​780,14.
   
6. 6
   Trække det nummer, du netop beregnet ud fra det aktuelle nummer på venstre side. I eksemplet, trække 329 fra 380, hvilket giver 51.
   
7. 7
   Gentag trin 4. Da du nu oplever kommaet i 780,14, skrive et komma i kvadratroden, øverst til højre. Drop det næste par (14) til venstre. To gange antallet øverst til højre (27) er 54, så skriv "54_ × _ =" i nederste højre kvadrant.
   
8. 8
   Gentag trin 5 og 6. Find den største ciffer at erstatte underscore og gøre det multiplikation. I eksemplet er 549 gange 9 4941, hvilket er lavere end eller lig med det antal til venstre (5114). Skriv 9 øverst til højre, og trække resultatet af multiplikationen fra tallet til venstre: 5114 minus 4941 er 173.
   
9. 9
   Hvis du ønsker at fortsætte med at beregne cifre, drop et par nuller til venstre, og gentag trin 4, 5 og 6.
   

Forklare processen

1. 1
   For at forstå, hvordan denne metode virker, overveje det nummer, du beregne kvadratroden af som området S af et kvadrat. Du forsøger derfor at beregne længden L af den side af kvadratet. Du ønsker at finde det antal L, således at L ² = S.
   
2. 2
   Antag, at du ringer til en det første ciffer af L (kvadratroden vi forsøger at beregne). B vil være dens andet ciffer, C sin tredje, og så videre.
   
3. 3
   Antag, at du kalder sa det første par cifre i s, sb det andet par cifre osv.
   
4. 4
   Ligesom i en afdeling, hvor du kun er interesseret i den næste ciffer ad gangen, her i calculus af kvadratroden, er du interesseret i de næste to cifre ad gangen (som er den næste ciffer ved en tid til kvadratroden). Og også, ligesom i en division, er placeringen af ​​kommaet ikke vigtigt i processen: Du kan altid bare tilføje det i slutningen.
   
5. 5
   Kig på det første par sa cifre i S (sa = 7 i eksemplet), og du ønsker at finde sin kvadratroden. Det første ciffer A i kvadratroden er da den største heltal, hvor pladsen ikke overstiger Sa (hvilket betyder en så A ² ≤ Sa <(A +1) ²). I eksemplet, S1 = 7, og 2 ² ≤ 7 <3 ², så A = 2.
   
6. 6
   Bemærk, at hvis du ønskede at opdele 88.962 med 7, det første skridt ville være ens: du ville se på det første ciffer af 88.962 (8), og du ønsker det største ciffer, når ganget med 7, er lavere end eller lig til 8. Hvilket betyder d så 7 × d ≤ 8 <7 × (d +1). d ville så være lig med 1.
   
7. 7
   Beregn næste ciffer B.
   
   • Overvej (10A + B) ² = 100A ² + 2 × 10A × B + B ². (Husk, at 10A + B er antallet med B i enhederne position og A i tiere position: med A = 1 og B = 2, 10A + B er simpelthen det nummer 12).
     (10A + B) ² er arealet af hele pladsen, 100 A ² (10A + B) ²> det område af største firkantet indeni, B ² er det område af den mindste firkant, og 10a × b B ²> er det område af hvert af de to rektangler.
8. 8
   I trin 3, trækker du en ² fra sa. At tage højde for faktoren 100, tabe dig et par (Sb) cifre i S: du vil "Sa Sb" for at være det samlede areal af pladsen, og man trækkes 100A ² (det område af store firkant) fra det. Hvad der mangler er antallet N1 opnået på venstre i trin 4 (380 i eksemplet). Og at antallet er lig med 2 × 10A × B + B ² (areal af de to rektangler plus areal af den lille firkant).
   
9. 9
   Kig efter n1 = 2 × 10a × b + b ², også skrevet som n1 = (2 × 10a + B) × B. Du kender N1 (= 380) og A (= 2), og du er på udkig efter B. I ligning er mest sandsynligt B ikke kommer til at være et heltal, så du skal faktisk finde den største heltal B, så (2 × 10A + B) × B ≤ N1. (Og B +1 ville være for stor, så du har:. N1 <(2 × 10A + (B +1)) × (B +1))
   
10. 10
    For at løse det, multipliceres A med 2, flytte den i position tiere (hvilket svarer til at multiplicere med 10), sted B i den position af enhederne, og formere sig, at antallet af B. Dette antal er (2 × 10A + B) × B, og det er præcis, hvad du gør, når du skriver "N_ × _ =" (med N = 2 × A) nederst til højre kvadrant i trin 4. Og i trin 5, finder du det største heltal B, der passer på underscore, så (2 × 10A + B) × B ≤ N1.
    
11. 11
    Fratræk området (2 × 10a + B) × B fra det samlede areal (på venstre side, som i trin 6), som giver dig det område s-(10a + b) ² endnu ikke tegnede sig for (og som vil blive brugt at beregne de næste cifre på en lignende måde).
    
12. 12
    For at beregne den næste ciffer c, gentag processen: drop det næste par (Sc) fra S for at få N2 til venstre, og se efter det største C, så du har (2 × 10 × (10A + B) + C) × C ≤ N2 (svarende til at skrive to gange den to-cifrede nummer "AB" efterfulgt af "_ × _ =" og kigge efter den største ciffer, der passer på underscore).